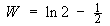ENGI 5432 Advanced Calculus
Final Examination, 2009 — Alternate Solution
Question 4(b)

  1. A vector field is defined on the xy plane by   F = (x+1) i^ x/(2-y)^2 j^
    A simple closed path   C   is defined by a triangle whose vertices are at the points (0, 0), (1, 0) and (0, 1).

    1. Find the exact value of the work done by   F   in one circuit of   C .

      [plot of triangle enclosed by path C] The work done may also be calculated using a direct evaluation of the line integral, but this involves three separate integrations and considerably more effort:

      Work done = Sum of three line integrals
       

      Along the path from O to A :
      applying parameter x=t, y=0
      line integral = 3/2

      Along the path from A to B, among many feasible parameterizations is:
      applying parameter x=1-t, y=t
      line integral = ln 2 - 2

      Along the path from B to O :
      applying parameter x=0, y=-t
      line integral = 0

      Adding the three contributions to the work done together, we find that
      W = 3/2 + (ln2 - 2) + 0

      work done = ln 2 - 1/2