ENGI 5432 Advanced Calculus
Final Examination, 2009
Alternative Solution to Q. 8

  1. For the partial differential equation

    2 u_xx + 11 u_xy + 5 u_yy = 4

    1. Find the general solution   u(x, y).

      lambda = -5 or -1/2
      The complementary function is   uc = f(y-5x) + g(y-x/2)
      The right side is a constant (zero-order polynomial) and the left side involves only second partial derivatives.
      Therefore try a second order polynomial as the particular solution:
      uP = ax^2 + bxy + cy^2
      [second derivatives of uP]
      Substituting these partial derivatives into the PDE:
      4a + 11b + 10c = 4
      This is an underdetermined system (only one equation for three unknowns), leaving a free choice for two of the three coefficients.   Let us make no assumption here about the values of the three coefficients, other than   4a + 11b + 10c = 4
      The general solution is the sum of the complementary function and the particular solution:

      u = f(y-5x) + g(y-x/2) + ax^2 + bxy + cy^2

    2. Using the additional information
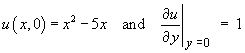
                    u(x,0) = x^2 - 5x , u_y(x,0) = 1
      find the complete solution   u(x, y).

      Starting with the form of the general solution found in part (b) above,
      du/dy
      f'(-5x) + g'(-x/2) + bx = 1 Equation 1
      u(x,0) = f(-5x) + g(-x/2) = (1-a)x^2 - 5x Equation 2
      -5 f'(-5x) - g'(-x/2)/2 = 2(1-a)x -5 Equation 3
      g'(-x/2) = (4/9 (1-a) - 10/9 b)x
      g(x) = 1/9(10b - 4(1-a))x^2
      Note that we can ignore the arbitrary constant of integration here.
      It will cancel out when the complete solution is assembled.
      Equation 2 ==> f(x) = (4(1-a)-b)/90 x^2 + x
      The complete solution is therefore
      u(x,y) = (y-5x) + 0 + x^2
      u(x,y) = (y-5x) + 0 + x^2
      u(x,y) = (y-5x) + 0 + x^2
      u(x,y) = (y-5x) + 0 + x^2
      But   4a + 11b + 10c = 4,   so that the coefficient of   y 2   is zero.
      The complete solution, regardless of the valid choice made for a, b, c, is

      u(x,y) = x^2 + y - 5x

      It is straightforward to check that this function satisfies both additional conditions and the partial differential equation.