ENGI 9420 Engineering Analysis
Mid Term Test Questions

2007 Fall
[Ordinary Differential Equations; Laplace transforms; Perturbation Series]
  1. Find the complete solution to the initial value problem

    x" + 10 x' + 21 x = 8 e^(-3t) , x(0) = 0, x'(0) = 2

    [10]

  1. Either

    Use the identities for Laplace transforms
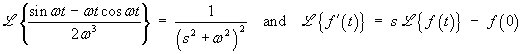
    L{(sin wt - wt cos wt) / (2w^3)} = 1/(s^2 + w^2)^2 and L{f'(t) = s L{f(t)} - f(0)
    to find L{t sin wt}

    [10]

    or

    Use the identities for Laplace transforms
    L{t f(t)} = -d/ds L{f(t)} and L{sin wt} = w / (s^2 + w^2)
    to find L{t sin wt}.

  1. Find the MacLaurin series solution of Airy’s equation

    y" + xy = 0

    with arbitrary initial conditions   y(0) = a,   y' (0) = b , as far as the term in x6.

    [10]

  1. The cubic equation
                  x^3 - 1.01x + 0.01 = 0
    is a special case (e = 0.01) of the perturbation
                  x^3 - (1+e)x + e = 0
    of the simple cubic equation
                  x^3 - x = 0
    Find the perturbation series, as far as the term in e2, for the root near x = –1 and hence find the solution of x^3 - 1.01x + 0.01 = 0
    nearest to x = –1, correct to four decimal places.

    [10]

  1. BONUS QUESTION:

    An over-damped mass-spring system is modelled by the ordinary differential equation

    x" + 3x' + 2x = 0

    where   x(t)   is the displacement of the centre of mass of the spring from its equilibrium position at time t.   The spring is released with velocity   vo   from location   x = +1   at time   t = 0.

    Find the condition on the initial velocity   vo   in order for the centre of mass of the spring to pass through its equilibrium position at some finite positive time   tc   and determine an exact expression for   tc   in terms of   vo.

    [+6]

    Return to the index of assignments [Return to the index of assignments]         [To the solution of this test] To the solution of this test
    Return to your previous page [Return to your previous page]