ENGI 9420 Engineering Analysis
Mid Term Test Questions

2008 Fall
[Ordinary Differential Equations; Laplace transforms; Perturbation Series]
  1. By any valid method, find the complete solution to the initial value problem

    (2xy + 4x) dx - (y+2) dy = 0 , y(0) = -2

    [10]

  1. By any valid method, find the function   y(t)   whose Laplace transform is
    Y(s) = 8 e^(-s) / [s^2 (s^2 + 4)]
    Hence (or otherwise) solve the initial value problem
    y" + 4y = 8(t-1) H(t-1) , y(0) = y'(0) = 0
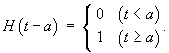
    where   H(t – a)   is the Heaviside (or unit step) function   H(t-a) = {0 for t < a ; 1 for t >= a}

    [10]

  1. Find the MacLaurin series solution of the ordinary differential equation

    y" + xy' - y = 1 + x^2

    with arbitrary initial conditions   y(0) = a,   y' (0) = b , as far as the term in x7.

    [10]

    BONUS QUESTION
    Find the condition(s) on   a   and/or   b   under which the series solution has only a finite number of non-zero terms and write down that finite series solution.

    [+6]

  1. The cubic equation
                  x^3 + 0.02x^2- 0.01x + 1 = 0
    is a special case (e = 0.01) of the perturbation
                  x^3 + 2ex^2 - ex + 1 = 0
    of the simple cubic equation
                  x^3 + 1 = 0
    Find the perturbation series, as far as the term in e2, for the root near x = –1 and hence find the solution of x^3 + 0.02x^2- 0.01x + 1 = 0 nearest to x = –1, correct to six decimal places.

    [10]

    Return to the index of assignments [Return to the index of assignments]         [To the solution of this test] To the solution of this test
    Return to your previous page [Return to your previous page]