Contents:
[Note: There was sufficient time to present sections 1-5, 7, 11 and 13 only.]
It is the fascinating concept of infinity that first drew me strongly to mathematics. The one other branch of science where infinity arises more clearly than any other is astronomy, especially within a black hole.
In the 1660’s, Isaac Newton contemplated the nature of gravity. His conclusions were eventually published in his epic work “Principia” in 1687. His vision of the Universe involves a framework of three dimensions of absolute space and one dimension of absolute time. In this model of reality, time passes at the same rate everywhere. An inverse square law governs the gravitational attraction between two point masses M and m, separated by a distance r:
![]()
where the constant of proportionality, G, is the universal
constant of gravitation, with a value in today’s SI units of
For most of everyday life here on Earth, Newton’s laws of gravitation and motion provide an adequate description of reality. It is often only at extremes of speed or gravity that one can detect deviations from predictions made using Newton’s laws.
|
Consider a test particle of mass m that is rising up from
a larger body of mass M. The particle’s upward
speed is v at any height r from the centre of the
larger body. In the Newtonian model, the particle’s
kinetic and potential energies are |
![[test particle m a distance r from the centre of M,
travelling away at speed v]](twomasses.gif)
|
The escape velocity from the surface of a spherical object of mass M and radius r is therefore
![]()
Sir Isaac Newton also believed that light consists of particles, not waves. [In the eighteenth and nineteenth century there was strong evidence for the wave-like nature of light. Quantum theory in the twentieth century indicates that light has the properties of both particles (“photons”) and waves.] In 1783, Rev. John Michell noted that if a sphere had sufficient mass packed inside a small enough volume, then the escape velocity would exceed the speed of light c:
![]()
Light itself would not be fast enough to escape from such a body, which would therefore appear totally black from a safe distance. Pierre-Simon Marquis de Laplace made a similar observation independently, some 16 years later. This critical radius has since become known as the Schwarzschild radius, rs.
For a mass of one kilogram, this critical radius is unimaginably
small:
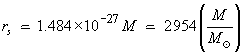
where ![]() is the mass of our Sun.
is the mass of our Sun.
But this consideration of escape velocity concerns freely falling bodies only. In Newton’s model of reality, one could still escape from this type of dark body by applying acceleration for long enough to escape.
Using the absolute frame of reference of Newton’s space-time, it became obvious that the speed of light emitted from objects moving at different speeds should be different. At the low speeds of our everyday experience, the addition law of velocities is obvious:
![[Train, speed v1, with object
on board at speed v2 relative to the train]](train1.gif)
The train has a speed v1 relative to an
observer standing beside the rail track.
Relative to an observer on the train, the block has a speed
v2.
Relative to the observer at the trackside, the block has a speed
v1 + v2.
The same should be true for light:
![[Train, speed v1, with lamp
on board shining light at speed c relative to the train]](train2.gif)
The stationary observer at the trackside should detect the light speed to be v1 + c.
Just how absurd this “common sense” line of reasoning is, can be seen by asking how fast the trackside observer will measure the speed of light directed backward down the train to be, when the speed of the train itself reaches the speed of light: the trackside observer should measure the light to have stopped altogether, then to start moving backwards as the train accelerates to faster than the speed of light.
In the nineteenth century, it was thought that there is an absolute frame of reference for space, know as the “æther”, which supports electromagnetic radiation. The Earth moves through the æther as it orbits around the Sun and as the solar system orbits the Galaxy and as the Galaxy moves through the Universe. The measured speed of light parallel to the velocity through the æther and at right angles should therefore be different. But when the experiment was performed in 1887 (the Michelson-Morley experiment), no such difference was found. The speed of light was found to be the same in every direction. The simple addition law for velocity is no longer true at speeds approaching the speed of light. |
![[Earth moving at speed v relative to the aether]](aether.gif)
|
In the 1970’s, at a sale by the public library of surplus books in Gloucester, England, I purchased a University physics textbook, (“Physical Optics” by Robert W. Wood, MacMillan, 1905) for just ten pence. The book was published well after the Michelson-Morley experiment but just before Einstein published his theory of special relativity. That textbook (on pages 518-520) does describe the null result of the Michelson-Morley experiment, does mention the Lorentz contraction (below), but has no explanation for it!
In 1905, Einstein published his special theory of relativity, which was founded upon the assumption that the speed of light in a vacuum is an absolute constant to all non-accelerating observers.
The addition law of velocities is modified from the simple
v = v1 + v2 to
![]()
or, equivalently,
![]()
which reduces to v = v1 + v2
when v1 and v2 are both
small compared to c.
For an object in motion at speed v relative to an observer,
the length in the direction of motion is shortened, mass increases
and time slows down by a factor
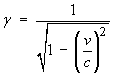 (the Lorentz factor).
(the Lorentz factor).
|
A one-metre long bar of rest mass 1 kg, travelling parallel
to its length at 60% of the speed of light relative to you,
is only 80 cm long and has a mass of 1.25 kg. A clock
travelling on that bar needs 75 of your seconds to register
one minute. When In many experimental particle accelerators, some elementary
particles are travelling so fast
|
![[One bar at rest, other at 60% c]](bars1.gif)
|
The muon is one species of subatomic particle that is created by very high energy collisions just above the atmosphere of Earth. Its lifetime is so short that, even near the speed of light, it should decay almost completely before it reaches the surface. Yet significant numbers do survive. From our point of view, time is running so slowly on the muons that they do not have enough time to decay before reaching the surface. From the point of view of the muons, however, they are at rest, with time running normally. It is the Earth that is rushing up to meet them. The Earth is approaching so fast that the depth of the atmosphere is contracted from hundreds of kilometres to only one kilometre or less. The muons have much less distance to travel, so more of them survive as far as the surface.
It is important to note that these effects of high speed are symmetric. When observers are travelling with each of two objects that are moving close to the speed of light in a constant direction with respect to each other, each observer will consider itself to be at rest. But each observer will deduce that the other object is shortened in the direction of motion, is more massive and has its clocks running slow. This leads to several famous “paradoxes”, which can be resolved with careful analysis. One such paradox is how to fit a 120 metre long runabout completely inside a 100 metre long spacedock hangar bay.
Represent one dimension of space on the horizontal axis and time vertically. Measure space and time in the same units (both in metres or both in seconds). Light travels nearly 300,000 km in one second, so one light-second is nearly 300,000 km. A nanosecond is just under 30 cm. A metre is just over 3.3 nanoseconds. The Sun is 499 seconds away from the Earth, because we see the Sun not as it is now, but as it was when the light set out some 8 minutes and 19 seconds ago (give or take 8 seconds). At this time of year [July], the Earth is near the aphelion of its slightly elliptical orbit around the Sun, so we are currently some 507 seconds away from the Sun.
|
Every event in space-time can be located with a set of
four coordinates, one for time and three for space.
The separation s of an event from your origin
is given by Notice the difference from the usual Euclidean formula
for spatial distance, |
|
Each point on these plots is not just a location, but a location and a time. The origin is here and now. To reach points on the vertical axis, we merely wait where we are. The separation s is then just the time (ct) that we have to wait to reach that event (our proper time). At the other extreme, events that can only be connected to each other by light signals have zero separation.
[Our frame of reference] |
Example: Measure all distances and times in years.
Some event A will occur five years from now, at a location
near the star Alpha Centauri, some 4 light years away.
The space-time separation of that event from here and now is We can influence that event because light has enough time
to reach that event Note that the locus [path] of all events that have the same
space-time separation of 3 years from here and now is not
the familiar circle from Euclidean geometry, but is instead a
hyperbola, intersecting the time axis at 3 years.
All such loci are hyperbolae, (except for
|
Any traveller who passes by us here and now with just the right constant velocity to reach the event four years away and five years in the future will need five years by our clock for the journey. However, the relative speed causes the clocks on the traveller’s spacecraft to run slow. The same journey requires only three years by the traveller’s clock.
Indeed, if the traveller passes by us here and now with just
the right constant velocity to reach any one event on the
locus
[Traveller’s frame of reference] |
From the point of view of the traveller, that person is at rest. It is we, the destination point four light years away and the space in between, that are rushing by at a significant fraction of the speed of light. . The initial spatial distance between the traveller and the destination point is shorter in the traveller’s frame of reference, some 2.4 years, (which requires three years to cover at 80% of the speed of light). On the traveller’s own space-time diagram, the traveller is stationary and therefore simply moving up her time axis for three years, until meeting the event. According to the traveller, we are rushing backward, with our clocks running slow. The traveller deduces that it takes us only three years on our clocks, but five years on the traveller’s clock, for us to reach event B. Note that the order in which events A and B occur is the other way around for the traveller! |
|
Note that the space-time separation is real only for events on or inside your light cone. Nothing can travel faster than the speed of light, so you can send signals (or travel) only to events inside your future light cone. You can see (and be influenced by) only events that are inside your past light cone. |
|
|
Light (and other electromagnetic radiation) can travel only on null trajectories. Objects with positive rest mass can follow only time-like trajectories. Space-like trajectories would be faster than light and would allow travel backwards in time as seen by some observers. This is one reason why space-like trajectories are considered to be impossible. |
Special relativity is a theory concerning motion in the absence of gravity. It took Albert Einstein another 11 years to formulate the theory of general relativity, on motion in a gravitational field.
Most stars shine by the energy produced from nuclear fusion
reactions. The simplest atomic element is hydrogen, which
has just an isolated proton for its nucleus. The end result
of various chains of reactions converts four protons into one
nucleus of the next element, helium. Every 1000 kg
of hydrogen is converted into 993 kg of helium, while the
other 7 kg is released as
![[illustration of the fusion of four protons
into a helium nucleus]](helium1.gif)
Those reactions require temperatures of millions of degrees to occur. Stars like our Sun convert more than half a billion tons of hydrogen into helium and light every second and continue to do so for billions of years before they run out of hydrogen fuel. At that point the star is mostly helium, at too low a temperature to fuse any further.
Approximately five billion years from now, our Sun will no longer produce enough pressure to support the vast weight of inert helium inside it. The helium sphere will start to collapse, becoming hotter, until it is hot enough to start fusing helium into heavier elements such as carbon and oxygen. The heat from the core collapse and from the new radiation blows the outer layers out so much that the Sun will transform into a red giant. Just before helium burning begins, the Sun will swell out so far that it will engulf Mercury, Venus and the Earth. The Sun will remain a red giant for perhaps a billion years.
The more massive a star is, the heavier the elements that can be created, (up to the limit of iron) and the faster it will use up its fuel.
A star like our Sun will reach a point where no further reactions are possible. With less pressure to support it, the Sun will contract under its own immense weight until the atoms are squeezed as closely together as possible.
A quantum phenomenon known as the Pauli Exclusion Principle becomes important. Essentially the electrons in the atoms literally have nowhere else to go. That degeneracy pressure will stop the collapse when the Sun is about the size of the Earth. The Sun will cool down slowly to an incredibly dense cinder and remain thereafter as a white dwarf star. A cubic centimetre of white dwarf matter would have a mass exceeding a ton.
If the mass of a white dwarf star exceeds 1.4 solar masses, however, then gravity overwhelms the electron degeneracy pressure, forcing the electrons down into the nuclei of the atoms against the powerful electric forces until most electrons have fused with most protons in the tiny atomic nuclei. This produces a very strange star composed almost entirely of neutrons and exotic subatomic particles, packed almost as close together as possible. When one considers that an atomic nucleus constitutes only a tiny fraction of the total volume of a normal atom, one can see that a further enormous compression occurs.
A collapse of this type normally occurs when a star several times more massive than our Sun tears itself apart in a colossal supernova explosion, although mass exchange between a red giant star and a close white dwarf binary companion might also trigger a collapse to a neutron star. The collapse can stop at the neutron star stage when the neutrons in their turn are packed as closely together as the Pauli Exclusion Principle will allow.
In a supernova, the collapse of an overweight degenerate iron core down to a neutron star is catastrophically rapid, less than a second. The suddenly unsupported surrounding layers of the stellar core fall inward and crash onto the surface of the rigid newly formed neutron star at an appreciable fraction of the speed of light. The resulting bounce is so strong that it tears most of the star apart with a power briefly exceeding that of a normal galaxy’s total output of light.
The density inside a neutron star is truly awesome. A mass which formerly occupied a sphere larger than the Sun, (more than a million kilometres across), has collapsed to a superdense state of diameter less than the width of St. John’s. One cubic millimetre of neutron star material has a mass of several thousand tonnes.
|
Gravity is so intense near a neutron star that Einstein’s theory of gravity must be used. Newton’s theory ceases to be accurate. One of the strange predictions made by Einstein is that gravity will pull light off a straight-line path. The scale in the diagram is exaggerated. The true position of the star is at A, but the observer detects it at B. For starlight passing very close to the Sun the effect is minute, less than a barely measurable two seconds of arc of deflection from a straight line. A famous expedition to observe a total solar eclipse, just after the First World War, made just such a measurement to verify this prediction. |
|
|
|
But light leaving at an angle of approximately thirty degrees to the true horizon from the surface of a neutron star that is barely stable will be bent so much that it will go into orbit. Light emitted at lower angles will be pulled right back onto the surface of the neutron star. To any probe on the surface of such a neutron star, the surface would appear to slope up to an horizon some thirty degrees above the horizontal and its line of sight would extend around the entire surface of the star. The sky on the opposite side of the neutron star would be visible just above the apparent horizon. |
The sphere around the neutron star at which photons can stay in an unstable circular orbit is called the photon sphere. It is located at 1.5 Schwarzschild radii from the centre of the star (as measured by a distant observer).
Imagine if you could survive the immense gravity and if you could blast your rockets hard enough to hover over the neutron star at a point on the photon sphere. What would you see?
|
The photon sphere would seem to be a bright infinite plane all around you. The surface of the star would fill the entire field of view below you - it would be a flat plane. What is true for light is also true for gravity, so there would no longer be any centrifugal force at all to help you maintain your orbit, no matter how fast you try to fly around the star. |
|
|
If you move up, above the photon sphere, then the star looks like an immense sphere, not a plane, so that some centrifugal force returns. The centrifugal force returns towards the value predicted by Newton’s theory of gravitation as one moves farther away from the star and as the warping of space-time becomes negligible. |
|
If you move down towards the surface, then the surface of the star curves up around you, so that the centrifugal force actually changes sign: the faster you travel around the star, the harder it is to avoid crashing down into the surface. There are therefore no unpowered circular orbits at all below the photon sphere. |
|
If a neutron star becomes more massive than 2.5 solar masses, then not even neutron degeneracy pressure will be able to resist the immense gravity. At that stage, no force known in nature can prevent a complete catastrophic collapse of the entire star down to a mathematical point. All the mass would be contained in a point of zero volume, infinite density and infinite gravity, known as a singularity. It seems impossible, yet the singularity is an inescapable consequence of the General Theory of Relativity, the best theory of gravity available today.
The mathematical details of a non-rotating black hole were established from the General Theory of Relativity by Karl Schwarzschild, just a few months after Einstein published the theory in 1916. In particular, the point of no return, the event horizon, occurs at the same place as where Newtonian theory predicts that the escape velocity reaches the speed of light, the Schwarzschild radius rs.
However, all known stars rotate and as they collapse they rotate faster. Our Sun needs one month to rotate once, but some neutron stars, (“pulsars”), are known to be spinning at several hundred revolutions per second. The pulsar at the centre of the celebrated supernova 1987A is spinning on its axis 1,968 times every second. The mathematical details of rotating black holes were derived from the complicated equations of General Relativity in 1963 by Roy Kerr.
|
A strange consequence of General Relativity is that a massive rotating body tends to drag space-time around with it. The effect is almost unmeasurably small for the Earth and the Sun, but it is extreme at a black hole. Inside the ergosphere everything is forced to rotate with the hole. Even light shining in the retrograde direction is swept along in the sense of rotation of the hole, relative to our frame of reference here on Earth. |
|
The parameter a is a multiple of the ratio of the angular momentum to the mass of the black hole and has a value between 0 (no rotation) and 1 (maximum possible rotation).
Side view of Kerr black hole (a = 0.8) |
Further in is the event horizon, beyond which we can see nothing at all. Theory suggests that there is an apparent horizon, called the Cauchy horizon. At the centre is the singularity, distorted by rotation into a ring. At the ring singularity all the known laws of physics cease to apply and strange things can happen. Fortunately the event horizon shields us from any view of the ring singularity. |
The extreme concentration of mass warps space-time so much that the light cones, within which all real matter is constrained to move, tip over. For a slowly rotating black hole, light directed radially outwards finds it harder and harder to escape from the black hole as the distance from the singularity decreases.
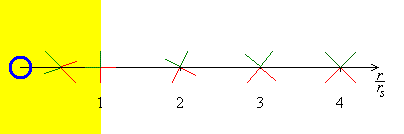
Close to the event horizon, most photons fall into the hole. Once inside the event horizon, the light cones have tipped so far over that even light directed outwards falls in to the singularity. Inside the point of no return, the radial dimension of space has effectively changed places with time: one can journey backwards in time as it is measured far from the black hole, but one cannot avoid travelling into the singularity in a finite time, just as, outside the event horizon, you cannot prevent today from becoming tomorrow.
For rotating black holes, a similar phenomenon occurs in the direction of rotation, so that nothing can stay at rest inside the ergosphere.
Even light travelling too close to the black hole in a direction opposite to the rotation of the hole (the retrograde direction) is forced to change direction upon entering the ergosphere.
|
The blue ray is initially falling radially inward, directly towards the black hole. The rotation sweeps it around somewhat. The first dark green ray also passes inside the static limit and falls into the black hole. The light green ray is at the critical distance from the black hole. It goes into orbit at the [inner] photon sphere. Any closer and it will plunge in through the event horizon. Any further away and it will escape. The other dark green rays are deflected, but do escape from the hole. The purple rays are travelling in a direction opposite to the rotation of the hole (the retrograde direction). Note that they have to be further away from the rotating black hole than the direct rays in order to escape. The red retrograde ray just barely escapes. If it were a little closer then it would be in an outer photon sphere for retrograde photons. |
Imagine viewing, from a safe distance, a small probe falling into a black hole. We would not notice anything unusual until the probe is within a few Schwarzschild radii of the centre of the black hole. The increasing speed of the falling vehicle would cause an increasing redshift, due to the Doppler effect.
A decrease in frequency (or, equivalently, a stretch in wavelength) of a photon is a redshift — the colour of the light shifts towards the red end of the spectrum. An increase in frequency (or, equivalently, a compression in wavelength) of a photon is a blueshift. Objects moving away from us at an appreciable fraction of the speed of light will be noticeably redshifted, while objects moving toward us will be blueshifted, (which is the Doppler effect for light). A similar Doppler effect for sound causes a siren to increase in pitch when approaching and to drop in pitch as it passes by us and recedes.
General relativity predicts that time slows down in a strong gravitational field, which also causes a redshift as seen from far away. It is only close to the event horizon that the gravitational effects would dominate.
Once inside the photon sphere, the probe would fade rapidly from view as its light shifts past the infrared. Also, the slowing of time relative to us would cause fewer and fewer photons to be emitted per second. In the case of a black hole ten times more massive than our Sun, the last photon would leave the doomed probe less than 0.01 seconds after crossing the photon sphere.
We would never see the probe cross the event horizon. According to our measurements, time stops completely at the event horizon, so that even the surface of the original collapsing star never quite crosses its own event horizon. However, it will fade completely and permanently out of view, very rapidly after collapsing past its photon sphere.
For a rotating black hole, our view would be further distorted by the dragging of space-time around it.
Instead of watching the probe from a safe distance, what would we see if we fell along with the probe?
For a black hole of ten thousand solar masses or less, we would not see much, because we would be torn apart by tidal forces long before reaching the event horizon. If you fall feet first, then your feet are approximately two metres closer to the singularity than your head. The difference in the gravitational force over such a short distance, even thousands of kilometres away from the black hole, is enough to kill.
For example, 5,000 km away from a fifty solar mass black hole,
(which is more than 30 Schwarzschild radii away), the difference
in the gravitational force over a distance of just two metres is
![[GM/r^2] at r=5000000 – at r=5000002](tide1.gif)
![]()
so that you are being stretched by a force more than twenty
times the strength of gravity on the surface of the Earth.
The general Newtonian expression for the tidal acceleration on a length L (metres) at a point x times further away from the singularity than the edge of the ergosphere of a black hole m times more massive than our Sun is approximately
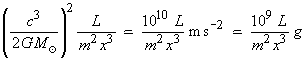
The only way for a human observer to survive tidal forces as far as the event horizon is to choose a supermassive black hole, anything above a million times the mass of our own Sun, for the journey. Such supermassive black holes may reside at the centre of most large galaxies, including our own.
Again the strong gravity distorts geometry and the vacuum paths of light rays. In the ergosphere everything would be swept around in co-rotation with the hole, including light from the outside Universe falling in after the observer. The rotation might not even be noticeable to the falling observer looking “straight up” out of the hole. There would be no extreme shifts in the wavelengths of light from outside even as the observer falls through the ergosphere and past the event horizon in a fairly short time, (a few hours or days for a galactic-mass black hole, much less than a second for a stellar-mass black hole).
The event horizon itself would be invisible and the doomed free-falling observer would notice nothing special upon falling through it. In the falling observer’s frame of reference, the event horizon is a light-like surface, which passes by the observer at the speed of light.

The situation is different if the observer descends slowly towards the event horizon, firing rockets furiously to stay above the event horizon. Once inside the photon sphere, going into orbit only increases the acceleration needed to resist the immense gravity of the black hole (because the highly warped geometry has caused the centrifugal force to change sign).
However, time slows down the closer one gets to the event horizon, which increases the gravitational acceleration that a stationary observer feels even more. At the event horizon, the acceleration needed to hold altitude above the singularity diverges to infinity. Also, the strong outward acceleration causes infalling light to become severely blueshifted and more energetic. The observer really does observe time passing more quickly in the outside universe, but in a small region of sky directly overhead, surrounded on all sides by the utter blackness of the hole.
Once past the event horizon, no amount of acceleration will stop the descent into the singularity - in fact such acceleration only hastens the end.
A freely falling observer will only notice strange effects close to the singularity, but by then the immense tidal forces will have torn any falling object apart.
|
The situation is somewhat different in a rotating black hole: at the inner (Cauchy) horizon time and space swap back again, allowing the observer to avoid the singularity. However, the encounter with the inner horizon is not survivable. All the matter and energy that will ever fall into the black hole all arrives at the inner horizon at the same instant. Looking up, the observer will see the entire history of the Universe play itself out to the end in a very short time, from light that becomes infinitely energetic. The inner horizon is no less lethal than the singularity of a non-rotating black hole. |
|
The story so far has been built on the foundation of one of the two greatest theories of twentieth century physics, General Relativity. The long term fate of black holes is governed by the other great theory, Quantum Mechanics.
In the 1970’s Prof. Stephen Hawking became convinced that black holes had to act as though they are black bodies, emitting random radiation at a temperature inversely proportional to their mass and with a power inversely proportional to the square of their mass.
|
In the vacuum, pairs of virtual particles are being
created and destroyed continuously, on time scales such
that the product of their energies and their lifetime is
less than a very small constant, (the Dirac constant
|
|
|
Very near the event horizon, a negative energy particle can fall into the hole, (thereby reducing the mass of the hole), while a positive energy real particle escapes. The overall effect is as if the hole were losing mass by emitting ordinary particles. The effect increases the smaller the hole is. |
The parameters for black hole evaporation are:
Blackbody temperature of a black hole of mass M (kg)
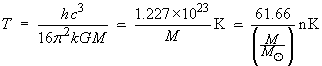
Emitted power of the evaporating black hole (Hawking
radiation only):
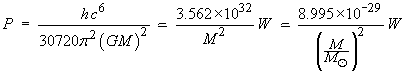
Lifetime of the black hole:
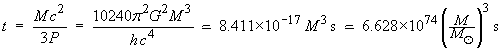
where
| speed of light | = c = | 299 792 458 m / s |
| gravitation constant | = G = | 6.67 × 10–11 N m2 kg–2 |
| Planck constant | = h = | 6.626 × 10–34 J s |
| Boltzmann constant | = k = | 1.381 × 10–23 J / K |
The lifetime can be deduced from the power by a simple definite integration:
The power P is a rate of change of energy,
E = M c2.
The mass M of the black hole is, in turn, a function of
the time t. Therefore
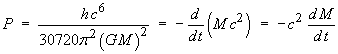
![]()
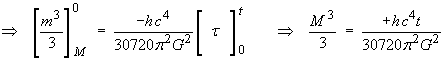
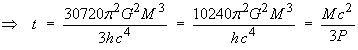
All black holes created by the collapse of stars have lifetimes immensely longer than the present age of the Universe, are very cold (less than a millionth of a degree above absolute zero) and emit negligible power (less than 10–28 W). For many billions of years to come, they will be absorbing mass faster than they emit it.
Only very tiny black holes (such as may have been formed in the first fraction of a second after the Big Bang) emit significant power. A one megaton black hole (the mass of a cube of water 100 m on each side) would have a radius much smaller than a proton, less than 10–17 m, would produce a gravitational acceleration of less than 1 g more than 9 cm away, would be immensely hot, over 1014 K (more than ten million times hotter than the centre of the Sun and hot enough to produce pairs of protons and antiprotons), with a power of 3.5×1014 W (corresponding to a mass loss of nearly 4 grammes per second). The hole would persist, becoming ever hotter and more luminous, for over 2,000 years.
The final 200 tonnes of mass would be radiated away in just over two thirds of a second, in a titanic explosion powerful enough to shatter the Moon.
Superb visualizations of space near a neutron star or a
black hole can be found on the web, at the sites of
Dr.
Robert Nemiroff and
Dr.
Andrew Hamilton.
My single favourite movie is of an orbit just above an
ultra-compact
Earth, on Dr. Nemiroff’s site.
An excellent introductory textbook on astronomy is “Universe” by W.J. Kaufmann III, (Freeman).
Another favourite textbook, suitable for the general reader, is
“Black Holes and Time Warps: Einstein’s
Outrageous Legacy” by K.S. Thorne, (Norton, 1994).
Also available here is an Excel spreadsheet file that displays the values of various black hole parameters for a chosen mass.