ENGR 1405 Engineering Mathematics 1

Faculty of Engineering and Applied Science
2000 Fall

Problem Set 8
Solutions

Note:   if you see symbols like ³ or Þ in various places, then your browser is not reading the style sheet for this Web page properly (or the Symbol font is not installed on your computer).   The translation is:

-   =   - (minus)

        Þ   =   Þ (implies)

Ö   =   Ö (square root)

        p   =   p (pi)

Ð   =   Ð (angle)

        q   =   q (theta)
  1. Find the Maclaurin series expansion and discuss convergence of the series for the function

But a quotable Maclaurin series is

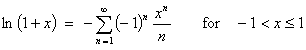
with absolute convergence on  -1 < x < +1 ,

conditional convergence at  x = +1

and divergence elsewhere.

Replacing  x by -x:

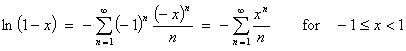
Combining the two series:

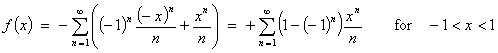
But

Therefore

The series is absolutely convergent for   -1 < x < 1   and divergent otherwise.

 

OR

 

From first principles,

 etc.

Upon examining the first few derivatives, one can deduce that

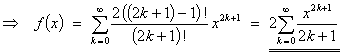
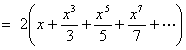
However, this method requires the use of the ratio test to determine the radius of convergence, followed by the limit comparison test at both endpoints  x = ±1 to determine the interval of convergence.

 

OR

 

 

 

Integrating term by term,

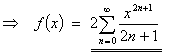
From the geometric series, absolute convergence is guaranteed for  | x | < 1 and divergence for | x | > 1.   However, the limit comparison test is needed in order to establish divergence at both endpoints  x = ±1.

 

  1. Express each of the following as a single complex number in the Cartesian form   z = x + j y:

a.        4 (5 - j3)   -   3 (2 - 7j)

 4 (5 - j3)   -   3 (2 - 7j)  =  20 - 12j  -  6 + 21j

=  14 + 9j

b.       (1 - 2j) (3 + 4j) / (4 + 3j)

(1 - 2j) (3 + 4j) / (4 + 3j)  =  (3 - 6j + 4j - 8j2) / (4 + 3j)

  =  (-11 - 2j) / (4 + 3j)

  =  (-11 - 2j) (4 - 3j) / [(4 + 3j) (4 - 3j)]

  =  (-44 - 8j + 33j + 6j2) / (16 + 9)

  =  1.52  -  1.64 j .

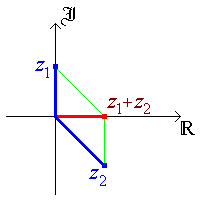
c.        (Ö2) ejp/2 + 2 e-jp/4

Addition is most easily performed in Cartesian form.

z  =  (Ö2) ejp/2 + 2 e-jp/4 

=  (Ö2) (cos(p/2) + j sin(p/2))  +  2 (cos(-p/4) + j sin(-p/4))  

=  (Ö2) j  +  2 ((Ö2)/2 - ((Ö2)/2) j)

=  (Ö2) j  +  (Ö2) - (Ö2) j

=  Ö2

This addition can be illustrated by a vector addition in an Argand diagram:

 

 

  1. Express each of the following as a complex number in the Euler form   z = r e jq   or using the phasor notation   z = r Ðq   [which is an abbreviation for the polar form   z = r (cos q + j sin q) ]:

a.      ((Ö3) - j) (1 + jÖ3)) / (1 - j)

Convert all three factors to phasor (or Euler) form.

 

 

 

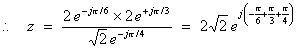
Therefore

 

OR

 

Remaining in Cartesian form,

(which is inadvisable given the required form of the answer):

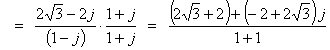
Þ    z  =  (1 + Ö3) + (Ö3 - 1) j

Þ   | z | 2 =  (1 + Ö3) 2 + (Ö3 - 1) 2

     =   1 + 2Ö3 + 3 + 3 - 2Ö3 + 1  =  8

Þ   | z | =  2Ö2

It takes some work, using trigonometric identities, to prove that

Arg z = 5p/12  exactly.

Therefore

            .

b.     Ö(12 - 9j)       (principal square root only)

z  =  Ö(12 - 9j)    Þ   z 2  =  12 - 9j  =  3(4 - 3j)

Þ   | z 2 | =  3 Ö(4 2 + 3 2)  =  3 ´ 5  =  15  

Arg (z 2)  =  Arctan(-3/4)

Þ    z 2  =  15 Ð (Arctan(-3/4) + 2np)     (n Î Z)

Þ    z   =  Ö(15) Ð (½Arctan(-3/4) + np)

The principal square root occurs at  n = 0 (or at any even value of n).

Therefore

 

OR

 

One can work in Cartesian coordinates instead:

z  =  x + yj  =  Ö(12 - 9j)

Þ   z 2  =  x 2 + 2xyj - y 2   =  12 - 9j

Equating real parts:

 x 2  - y 2   =  12

Equating imaginary parts:

2xy  =  - 9

Also  x  and  y  must both be real numbers.

The real solution to this pair of simultaneous non-linear equations can be shown to be

(x, y)  =  ±(Ö13.5, -Ö1.5)

The principal square root  z  must be such that  Re(z) ³ 0.

Therefore   z  =  (Ö13.5)  - (Ö1.5) j

Þ   | z | =  Ö(13.5 + 1.5)  =  Ö15

and   Arg z  =  Arctan(-Ö(1.5/13.5))  =  Arctan(-1/3)

Therefore

[By use of the formula for tan 2q, one can show that

Arctan(3/4)  =  2 Arctan(1/3).]

  1. Use deMoivre’s Theorem to express
    1. tan 4q   in the form of a ratio of functions which involve powers of   tan q;

Using deMoivre’s Theorem with  n = 4:

cos 4q  +  j sin 4q  º  (cos q  +  j sin q)4 

Let  c  º  cos q  and  s  º  sin q, then

cos 4q  +  j sin 4q  º  c4  +  4c3(js)  +  6c2(js)2  +  4c(js)3  +  (js)4 

Equating real parts:

cos 4q  º  c4  -  6c2s2  +  s4 

Equating imaginary parts:

sin 4q  º  4c3s  -  4cs3

Therefore

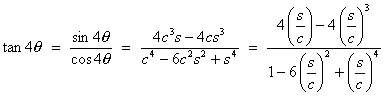
    1. csc 4q   in the form of a ratio of functions which involve powers of   csc q.

But  csc q  =  1/s   and   c2  =  1 - s2, so

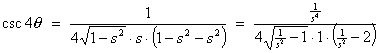
Therefore

 

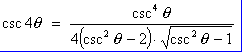
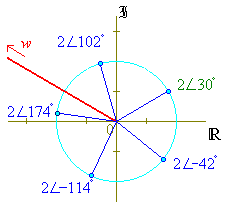
  1. By using deMoivre’s Theorem determine all distinct values of   z   in the Cartesian form   

z = x + j y , where:

a.      z5 = -16(Ö3) + 16 j

Let w = -16*sqrt{3} + 16j then |w| = 32
and Arg(w) = (180-30)deg

[Note:   w is in the second quadrant of the Argand diagram, but   Tan-1x is in the fourth quadrant when x < 0.   Therefore 180° must be added to the principal value of the inverse tangent function in order to place the argument in the correct quadrant.   A correction of ±180° must be made to the argument whenever the real part is negative.]

[Argand diagram]

The full equation to be solved is, in phasor form,
z^5 = 32*Angle(5*pi/6 + 2*k*pi)
where k is any integer.
r = 2, , theta = (5 + 12k)*pi/30
or, in degrees,   q = (5 + 12k) × 6°
The principal solution occurs at k = 0.
A set of five distinct solutions is obtained from any five consecutive values of k, such as
k = -2, -1, 0, 1, 2.   The arguments of consecutive solutions are separated by (360°/5 =) 72°.
In phasor form, an exact solution set in radians is
z = {2*Angle(each of {-19, -7, 5, 17, 29}*pi/30)}
and in degrees is
z = {2*Angle(each of{-114, -42, 30, 102, 174}deg)}

Correct to three decimal places, the five distinct solutions in Cartesian form are:

z = { -0.813 -1.827j , 1.486 -1.338 j , 1.732 + j ,

-0.416 + 1.956 j , -1.989 + 0.209 j }.

Argand diagram of the five solutions

 

b.     z1/3 = 0.6 - 0.8 j

Let   w  =  0.6 - 0.8 j, then  | w |  =  Ö(.62 + .82)  =  1

and   Arg w  =  Arctan (-4/3)  »  -53.130°

The equation to be solved is

z1/3 = w    Þ   z  =  w3  =  1 Ð(3´(-53.130°+360k°)),

where  k  is any integer.

There exists only one distinct solution, with principal argument at k = 0:

z  =  1 Ð-159.39°

Correct to three decimal places, the Cartesian form of this solution is

z  =  -0.936 - 0.352 j

[By using various trigonometric identities, it can be shown that this answer is, in fact, exact!  :   z  =  -(117 + 44j) / 125]

 

OR

 

An alternative method is to stay in Cartesian form throughout:

x + jy  =  (0.6 - 0.8 j)3  =  (3  -  4 j)3 / 53  

=  ((3)3  +  3(3)2(-4j)  +  3(3)(-4j)2  + (-4j)3 ) / 125

=  (27  -  108 j  -  144  +  64 j) / 125

Therefore

z  =  (-117  -  44 j) / 125

c.      z2 + 12 z = -32 + 4 j

Solving the quadratic equation:
z2 + 12 z = -32 + 4 j
Þ z2 + 12 z + 32 - 4 j = 0
[quadratic formula]
z = -6 +- 2*sqrt{1+j}

Completing the square:
(z + 6)2 = z2 + 12 z + 36
Þ (z + 6)2 - 36 = -32 + 4 j
Þ (z + 6)2 = 4 + 4 j = 4 (1 + j)
z = -6 +- 2*sqrt{1+j}

But sqrt{1+j} = 2^(1/4)Angle(pi/8)
[polar form]
z = -6 +- 2^(5/4)cos(pi/8) + j*2^(5/4)sin(pi/8)
Correct to three decimal places:

      z = -8.197 - 0.910 j ,         -3.803 + 0.910 j      

[You can confirm these values using the QBASIC program "quadgen.exe" (source code also available).]

 

d.     z4 + (4 + 4j) z3 + (12 j) z2 - (8 - 8j) z - 20 = 0

z4 + (4 + 4 j) z3 + (12 j) z2 - (8 - 8 j) z - 20 = 0               --(1)

Note that   (z + c) 4 = z4 + 4 c z3 + 6 c2 z2 + 4 c3 z + c4
Let   c = 1 + j , then
c2 = 1 + 2 j + j2 = 2 j
c3 = c c2 = (1 + j) (2 j) = - 2 (1 - j)
c4 = c2c2 = 4 j2 = -4

Þ     (z + (1 + j)) 4 = z4 + (4 + 4 j) z3 + (12 j) z2 - (8 - 8 j) z - 4
Þ     Equation (1) is
(z + (1 + j)) 4 - 16 = 0
(z + (1+j))^4 = 16 = 2^4*Angle(2*pi*k), where k = any integer
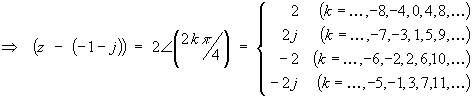
z - (-1-j) = {2, 2j, -2 or -2j

Therefore

      z   =   1 - j ,   -1 + j ,   -3 - j   or   -1 - 3 j      

Additional note:

The four distinct solutions all lie on a circle in the Argand diagram, centre   z = - 1 - j , radius 2.   They are symmetrically placed, 90° apart from each other.   All four solutions satisfy the equation | z - (-1 - j) | = 2 (which is the equation of the circle in the Argand diagram).

[Argand diagram]

Checking one of the four solutions [not essential]:

If   z = -3 - j, then
z2 = 8 + 6 j ,
z3 = -(8 + 6 j) (3 + j) = -18 - 26 j, and
z4 = (8 + 6 j)2 = 28 + 96 j.

Substituting into the left side of equation (1):
(28 + 96 j) + (4 + 4 j) (-18 - 26 j) + (12 j) (8 + 6 j) - (8 - 8 j) (-3 - j) - 20
= (28 + 96 j) + (32 - 176 j) + (96 j - 72) + (32 - 16 j) - (20)
= 0 + 0 j               Ö

 

  1. Express the complex number   z = uw   in the form   z = x + jy   when

u = 1 - j     and     w = (Ö3) - j

[Hint:   Write the complex number   "u"   in the Euler form   u = r e j(q + 2kp) = e (ln(r) + j(q + 2kp)),   then use the normal rules for multiplying exponents and then use de Moivre’s Theorem.]

In general, to evaluate   uw   where the exponent   w   is non-real, express the base   u   in Euler form (with the magnitude expressed as a real exponential function) but express the exponent   w   in Cartesian form.

u = 1 - j = sqrt{2}Angle(-45+360k)deg
= exp(ln(sqrt{2}) + j(-pi/4 + 2*k*pi), where k = any integer.

w = sqrt{3} - j
u^w = ...

u^w = R e^(jT) = exp(sqrt{3}ln(sqrt{2}) + 2*k*pi - pi/4) * exp(j*((2*k*pi-pi/4)*sqrt{3} - ln(sqrt{2}))
where R = |u^w| = exp(sqrt{3}ln(sqrt{2}) + 2*k*pi - pi/4)
and T = arg(u^w) = exp(j*((2*k*pi-pi/4)*sqrt{3} - ln(sqrt{2})), where k = any integer.

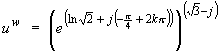
The Cartesian form is
uw = x + j y = (R cos Q) + j (R sin Q)
This generates an infinite family of solutions, four of which are shown (correct to the number of decimal places showing) in the table below.   The principal solution occurs when k = 0.

k R Q x y
-1 0.001551861 -12.5897 0.001551438 -3.6231E-05
0 0.831008632 -1.70692 -0.112773489 -0.82332101
1 444.9981882 9.175873 -431.2845791 109.6220749
2 238292.8165 20.05867 84319.63659 222875.8966

These values were generated by an Excel97 spreadsheet.
An updated spreadsheet to calculate a general   uv   is also available.

 

  1. Show that   j j = (Ö-1)(Ö-1)   is real and find its principal value.

j = e^(j*pi/2) = e^(j*(pi/2 + 2*k*pi))
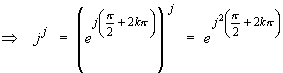
==> j^j = (e^(j*(pi/2 + 2*k*pi)))^j
= e^-(pi/2 + 2*k*pi), where k is any integer.
This is an infinite set of real numbers.
The principal solution occurs when k = 0.
The principal value of   j j   is therefore e-p/2 » 0.2079.

 

Back to the Index of Problem Set Questions  [Back to the Index of Problem Set Questions]
Back to the solution page  [Back to the Index of Solutions]
  [Return to your previous page]

Created 2000 11 20 and modified 2000 11 22 by Dr. G.H. George