ENGR 2422 Engineering Mathematics 2
An Example
using Jacobians in Multiple Integration
A
major application of the Jacobian (Section 2.4 of the
course notes) is to multiple integration over areas or volumes (Chapter 6).
Example:
A
solid sphere of radius 2 m and centre at the origin has a non-uniform density
given (in SI units) by
, where r is the distance from the point (x,
y, z) to the origin.
Find
the mass of the sphere.
For
uniform density, the mass m of an object of volume V
is just m = rV.
For
non-uniform density, the mass is 
Cartesian
coordinates are appropriate if the volume is a cuboid, in which case
dV = dx
dy dz.
But
for a sphere the limits of integration become very awkward unless the integral
is transformed into spherical polar coordinates, for which
dV = r2 sin
q dr dq df, (where r2 sin q is the Jacobian of the transformation from
Cartesian to spherical polar coordinates).
In
this example,
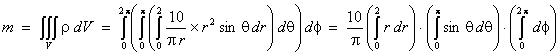
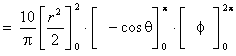
Therefore
the mass of the sphere is
|
m =
80 kg. |
Note that the mass is finite even though the density increases without bound as one approaches the origin!
[Return to your previous page]