ENGI 5432 Advanced Calculus

    Faculty of Engineering and Applied Science
    2009 Winter

    Problem Set 7   -   Questions

    [Sections 1.7, 2.6]
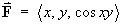    1. Show that no potential function exists for the vector field   F = < x, y, cos xy >.
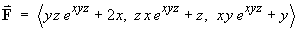
    1. For the vector field   F = < yz exp(xyz) + 2x, zx exp(xyz) + z, xy exp(xyz) + y >
      1. Show that a potential function   V(x, y, z)   does exist.
      2. Find the potential function   V(x, y, z)   that is defined in such a way that the potential is zero at the origin.
    1. For the vector field
      F = < x, y, z > / (r exp(r)) , where r = sqrt{x^2 + y^2 + z^2}
      is the distance of the point (x, y, z) from the origin):
      1. Show that a potential function   V(x, y, z)   does exist.
      2. Find the potential function   V(x, y, z)   that is defined in such a way that the potential is zero at infinity.   [Hint:   work in spherical polar coordinates.]
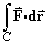
      3. Hence evaluate the line integral   integral_C {F dot dr}
        where   C   is the arc of   { 700x2 + 225z2 = 144,   y = -0.6 }   between the points (0.3, -0.6, 0.6) and (0, -0.6, 0.8).
        [You may leave your answer in terms of powers of   e.]
      4. Find the absolute maximum and absolute minimum values of the potential function   V.
      5. What type of curve is   { 700x2 + 225z2 = 144,   y = -0.6 }?
    1. Parabolic cylindrical coordinates are defined by
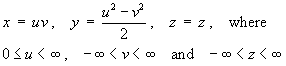
      x = uv , y = (u^2 - v^2) / 2 , z = z , where 0 <= u < oo , -oo < v < oo and -oo < z < oo
      As in question 5(d) of Problem Set 5, the cross-sections of the coordinate “planes” in the x-y plane are parabolas intersecting each other at right angles.   The coordinate surfaces   u = uo   and   v = vo   are therefore vertical parabolic cylinders intersecting each other at right angles, while the third set of coordinate surfaces are the familiar horizontal planes   z = zo.
      1. Determine the scale factors   hu , hv , hz .
      2. Hence find the expression for the volume element   dV = dx dy dz   in terms of the differentials   du dv dz.
        [The term multiplying   du dv dz   is the Jacobian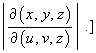 | partiald(x,y,z) / partiald(u,v,z) |
      3. Determine the gradient vector   Ñf (u, v, z).
      4. Determine the Laplacian   Ñ2f (u, v, z).
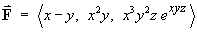    1. Calculate the circulation of   F = < x-y, x^2 y, x^3 y^2 z exp(xyz) >   counterclockwise around the unit circle in the xy-plane.   [Hint:   Use Stokes’ theorem, letting the surface   S   be any smooth surface that has   C   as its boundary.]
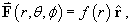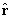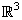    1. Consider the purely radial vector field   F(r,t,f) = f(r) rHat   where   unit vector rHat   is the unit radial vector in the spherical polar coordinate system and   f (r)   is any function of   r   that is differentiable everywhere in real 3-space (except possibly at the origin).
      1. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the divergence of F.
      2. Find an expression, in terms of   r,   f (r)   and   f ' (r), for the curl of F.
      3. Is   F   a conservative vector field?
      4. Of particular interest is the central force law
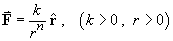
        F = (k/r^n) er (k, r > 0)
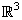        Show that the divergence of   F   vanishes everywhere in real 3-space (except possibly at the origin) if and only if   n = 2 .
        [Two of the four fundamental forces of nature, electromagnetism and gravity, both obey this inverse square law.]
    1. An extended source of electric charge has a charge density
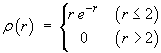
      rho = r exp(-r) , (r <= 2) ; 0 , (r > 2)
      where   r = the distance of the point (x, y, z) from the origin.
      1. Find the total charge   Q   due to this extended object.
      2. Find the total flux due to the extended charge through the simple closed surface   S   defined by   (x-3)2 + (y-4)2 + z2 = 1.

    1. For the vector field   F   =   e- k r r,   where 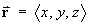vector r = < x, y, z >   and   k   is a positive constant,

      1. find the divergence of   F .
      2. find the curl of   F .
      3. find where   div F = 0   and classify this surface.
      4. find where the magnitude   F   of the vector field   F   attains its maximum value.
      5. show that 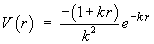  V(r) = - (1 + kr) / k^2 * exp(-kr)   is a potential function for the vector field   F.
      6. find the work done to move a particle from the origin to a place where   div F = 0.

      Return to the Index of Problem Sets   [To the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
      Back to previous page   [Return to your previous page]
    Created 2008 01 01 and most recently modified 2008 12 27 by Dr. G.H. George